- Читать практическое задание online по теме 'Проектирование планетарного редуктора'.
- Обзор механизмов с центральными колесами и водилом. Методика кинематического расчета.
Размещено на РАСЧЕТ ПЛАНЕТАРНОГО РЕДУКТОРА Введение Планетарным зубчатым называют механизм, содержащий зубчатые колеса с перемещающимися осями, именуемые сателлитами. Передача (рис.1) состоит из центрального колеса с наружными зубьями (солнечной шестерни) (1), центрального колеса с внутренними зубьями (3), водила (H) и сателлитов (2). Сателлиты устанавливаются в водило H, ось вращения которого называется основной.

Расчёт планетарной передачи. (редуктор Джеймса. (программа ТМ22. Коллеги, не подскажете ли программу для расчёта планетарного редуктора? Когда-то у меня.
Для краткого обозначения планетарных механизмов широко используются классификационные формулы, в которых указывается число и вид основных звеньев. Механизмы 2А-h (рис. 1) это планетарные механизмы с одновенцовыми сателлитами, у которых в качестве основных звеньев имеются два центральных колеса и водило. Кинематическая схема планетарного редуктора: 1- центральное колесо с наружными зубьями; 2- сателлитов; 3- центральное колесо с внутренними зубьями; Н - водило Задание Спроектировать планетарный редуктор по схеме, показанной на рис. Момент на выходном валу редуктора Т = 260 н.м.
Передаточное отношение редуктора i р = i 1 H (3) = 6. Угловая скорость ведущего вала щ 1 = 230 рад/с. Режим работы - средний нормальный, время работы передачи- t = 10000 ч. Кинематический расчет 1.1 Определение чисел зубьев колес Уравнение для определения числа зубьев редуктора Z 1:Z 2:Z 3:=1:( i 1H (3) -2)/2:( i 1H (3) -1): i 1H (3) /n w, где - z 1 число зубьев солнечной шестерни; z 2-число зубьев сателлитов; z 3- число зубьев центрального колеса с внутренними зубьями; n w -число сателлитов; -целое число. Принимаем число сателлитов n W = 3, что должно обеспечить получение компактной конструкции и равномерность распределения нагрузки по сателлитам. I 1 H (3) - передаточное отношение редуктора.
Обозначение передаточного отношения, связывающего относительные угловые скорости двух звеньев, имеет три индекса: два внизу, соответствующие обозначениям этих звеньев (первый из них относится к звену, угловая скорость которого в числителе), и один вверху, соответствующий звену, относительно которого взяты угловые скорости. Например, запись i 1 H (3) означает передаточное отношение между звеньями 1(центральным колесом с наружными зубьями) и H (водилом) в движении относительно колеса 3 (центральным колесом с наружными зубьями), которое неподвижно. Передаточное отношение имеет знак плюс, если направления вращения связываемых им звеньев совпадают.
При i 1 H (3) = 6 уравнение для определения числа зубьев редуктора будет выглядеть Z 1:Z 2:Z 3:= 1: 4/2: 5: 6/3. Числа зубьев колес выражаем через z 1 - число зубьев центрального колеса: z 3 = (i 1H (3) - 1) z 1 = (6-1) Z 1 = 5Z 1; z 2 = (i 1H (3) /2 - 1)z 1 = (6/2 -1) Z 1 = 2Z 1; г = (i 1 H (3) / n w)z 1 = 6/3 Z 1 = 2Z 1. Подбором (учитывая при этом, что должно соблюдаться неравенство z 117) находим, что z 1, z 4 и г будут целыми числами при z 1 = 18; z 3 = 90; z 2 = 36. 1.2 Проверка правильности выбора чисел зубьев При проектировании планетарных передач следует соблюдать три условия собираемости: 1.

Условие соосности валов центральных колес. Для этого в передачах, выполненных без смещения производящего контура, число зубьев колес должно удовлетворять условию z 3=z 1+2z 2. В передачах со смещением производящего исходного контура условие соосности проверяют равенством межосевых расстояний колес: А w 12=А w 23, где А w 12 -межосевое расстояние между сателлитом 2 и солнечным колесом 1; А w 23 -межосевое расстояние между сателлитом 2 и корончатым колесом 3. Вхождение зубьев в зацепление при равных углах расположения сателлитов. Для этого сумма чисел зубьев колес 3(корончатого) и 1(солнечного) должна быть кратна числу сателлитов: z 3+z 1/n w=, где n w-число сателлитов; - целое число.
Условие соседства. Необходимо, чтобы соседние сателлиты не задевали при вращении зубьями друг друга: d a22. 1.3 Определение угловых скоростей При исследовании кинематики планетарных передач широко используют метод остановки водила- метод Виллиса.
Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от 1 к 3 через паразитные колеса 2: i 3 1 H =1+z 3/z 1 = 1+90/18= 6. Угловая скорость водила (абсолютная): Н (3) = 1 / i 1 H (3) = 210/6= 35 с -1.
N Н (3) =30. Н (3)/= 30.35/3,14=334,23 об/мин. Угловая скорость солнечного колеса в относительном движении: 1 (Н) = 1 - Н = 210-35 =175 с -1. Передаточное отношение между солнечным колесом и сателлитом в относительном движении (при остановленном водиле): i 12 ( H ) = Частота вращения солнечного колеса: об/мин. Частота вращения сателлита: об/мин. Относительная угловая скорость сателлита: с -1. Определение КПД передачи и вращающих моментов 2.1 Определение КПД Принимаем для всех опор подшипники качения.
Для двух ступеней передачи (с внешним и внутренним зацеплением) при остановленном водиле з 13 ( H )=0,98.0,99=0,970 КПД планетарной передачи: КПД редуктора с учетом потерь в двух парах подшипников, для каждой из которых з n = 0,99, 2.2 Номинальный момент на ведущем валу Н.м. Расчет зубчатого зацепления на прочность 3.1 Выбор материала и допускаемые напряжения 3.1.1 Выбор материала Используя рекомендации работ 1, 3, выбираем для солнечной шестерни и сателлитов сталь 40 ХН, термообработка улучшение. Их механические характеристики определяем по табл. При предполагаемых диаметрах заготовки до 120 мм твердость поверхности зуба и для солнечной шестерни, и для сателлита 270 НВ. 3.1.2 Допускаемые контактные напряжения Допускаемые контактные напряжения 3,. 5 (1) где j = 1 для солнечной шестерни и j = 2 для сателлита, у Hlim bj - предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов перемен напряжений, определяется в зависимости от марки стали и ее химико-термической обработки 14, табл. 6 Предел контактной выносливости: у Hlim b 1=у Hlim b 2= 2HB 2 cp+70=2.270+70=610 МПа.
S H - коэффициент безопасности. S H = 1,1 для колес с однородной структурой материала, S H = 1,2 при поверхностном упрочнении зубьев 4, табл. Для солнечной шестерни и сателлита S H 1 = S H 2 =1,1. K HLj - коэффициент долговечности: K HLj = 6 N j но / N не j 1, 4,. 38 где N не j - эквивалентное число циклов напряжений; N но j - базовое число циклов, определяемое в зависимости от твердости (по Бринелю или Роквеллу), N но = 30(НВ) 2,4 340 (HRC) 3.15 + 8.10 6. При HRC 56 принимают N но = 1,2.
10 8. N но1=N но2 = 30 (HВ 2ср ) 2,4 = 30.270 2,4 = 2,05.10 7.
Величина N не j определяется по формуле: N не j = N j. К не, где К не - коэффициент приведения переменного режима работы к постоянному, определяется в зависимости от заданного режима работы 3, табл. 4 К не = 0,18; N j = суммарное число циклов напряжений: Для солнечной шестерни: N У 1= 60.t У.n 1.n w=60.,35.3=3,6.10 9 N He 1= N У 1.K He=3,6.10 9.0,18 = 6,48.10 8. Для сателлита: N У 2=60.10000.835,56 =5,01.10 8. N He 2= N У 2. K He =5,01.10 8.0,18=9,02.10 7. Принимаем для солнечной шестерни К HL 1 = 1, для сателлита К HL 2 =1 Определяем: МПа.
В случае расчета прямозубых передач допускаемое контактное напряжение у HP принимается равным у HPj min, т.е. Минимальному из двух значений, вычисленных по формуле (1) Окончательно принимаем у HP=550 МПа. 3.1.3 Допускаемые напряжения изгиба Из-за конструктивных трудностей, связанных с осевыми силами косозубые зубчатые колеса в планетарных передачах не используют. Поэтому мы будем рассматривать расчет только прямозубых колес. Допускаемые напряжения изгиба 3,.
18, (2) где у Flim b - предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемен напряжений, определяется в зависимости от марки стали и ее химико-термической обработки 11 табл. 4 3, с.16; у F lim b 1= у F lim b 2=1,35.НВ 2ср+100=1,35.270+100=465 МПа S F - коэффициент безопасности, S F = 1,65 S F `, где S F ` - коэффициент, учитывающий способ получения заготовки зубчатого колеса (для поковок и штамповок S F `= 1), S F 1= S F 2=1,65; K F L - коэффициент долговечности:, при НВN FO принимаем К FL=1. K F С - коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При нереверсивной (односторонней) нагрузке 3,. 15 K F С = 1.
При реверсивной симметричной нагрузке: K F С = 1 - г F С, где г F С - коэффициент, учитывающий влияние химико-термической обработки. В соответствии с 11 табл. 13 и для солнечной шестерни и для сателлита: К F С1=1; К F С2=1-0,35=0,65; Определяем у FPj по формуле (2).
3.2 Определяем межосевое расстояние между солнечным колесом и сателлитом Ориентировочно рассчитываем величину межосевого расстояния 6, с.3 (3) где BA - коэффициент ширины венца по межосевому расстоянию, который выбирают из единого ряда, рекомендованного ГОСТ 2185-66 11, табл. 3, принимаем ш ВА=0,25; n w -приведенное число сателлитов (с учетом неравномерности распределения нагрузки между ними), n w = n w -0,7=3-0,7=2,3; u-передаточное число, отношение числа зубьев большего колеса рассчитываемой пары (в нашем случае сателлита) к меньшему (в нашем случае солнечной шестерни) u 2=z 2/z 1= 36/18= 2. Т 1-вращающий момент, Т 1= 260 нм, H Р -допускаемое контактное напряжение, у НР=550 МПа; K H - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; коэффициент ширины венца по диаметру Ш bd=0,5.ш ba.(u 2+1)=0,5.0,25.(2+1)=0,375. По 11, табл. 8 определяем, что при НВ.
Целью данной работы являлось проектирование и расчет редуктора с помощью программной среды KISSsoft/KISSsys. В качестве исходных данных имеем схему конструкции редуктора и выходные значения мощности и оборотов вала. Схема представлена на рис. Редуктор включает в себя червячную, цилиндрическую и коническую передачи.
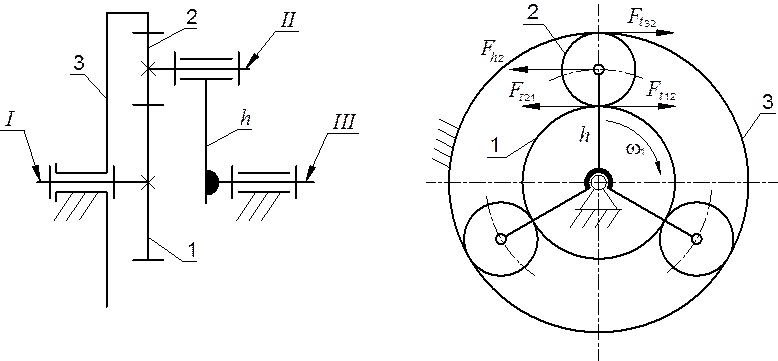
Расчет Планетарного Редуктора Программа
Между цилиндрической и конической передачами, а также между валом электродвигателя и входным валом редуктора установлены упругие муфты. Поток мощности подается на червяк. Снимается мощность с колеса конической передачи. Выходное значение мощности равно 5 кВт при частоте 9 об/мин, ресурс 7500 ч.
Схема конструкции редуктора Ход работы Проектирование началось в модуле KISSsysс создания группы, включающей 5 валов. Для каждого вала создаются входящие в него элементы: подшипники, зубчатые колеса, муфты и т.п.; задаются нагрузки. Также в состав включаются расчеты самого вала, подшипников, шпонок, шлицевых соединений и пр.
Затем добавляются связи между элементами. 2 изображен пример задания связи для упругой муфты. Определение элементов связи упругой муфты Далее определяются подвод и отвод мощности. 3 представлено окно задания выходных параметров редуктора.
Задание выходных параметров редуктора Когда все условия определены, производится расчет кинематики редуктора. Также отображается кинематическая схема согласно заданным параметрам (рис. Схема редуктора Затем выполняются расчет редуктора в программе KISSsoft: расчет зубчатых передач (рис. 5), расчет валов (рис. 6), расчет подшипников (рис. 7), расчет шпоночных и шлицевых соединений.
Расчет цилиндрической зубчатой передачи в интерфейсе KISSsoft Рисунок 6. Расчет вала червячного колеса (быстроходного вала цилиндрической зубчатой передачи) Рисунок 7.
Расчет Планетарного Редуктора Программа
Расчет подшипников тихоходного вала цилиндрической зубчатой передачи После выполнения расчетов добавляется 3D-вид спроектированного редуктора. Затем выполняется позиционирование валов друг относительно друга: задание координат (в полярной или декартовой системе координат); позиционирование по зубчатой цилиндрической/зубчатой конической/червячной передаче (указываются значения межосевого расстояния, угла взаимного расположения валов и угла контакта); параллельно двум валам/валу или группе.
Когда позиционирование валов завершено, отображается уже законченная модель редуктора (рис. Есть возможность задавать цвета деталей и компонентов. Трехмерная модель спроектированного редуктора Готовую модель можно экспортировать в большинство CAD-систем: SolidWorks, ProENGINEER, CATIA и некоторые другие. 9 изображен спроектированный редуктор, экспортированный в среду ProENGINEER как сборка, каждый элемент можно открыть, редактировать и сохранить как отдельную деталь (рис. Сборка редуктора в ProENGINEER Рисунок 10. Драйвер для флешкарты sd. Червяк в среде ProENGINEER В созданный проект можно добавить пользовательский интерфейс - таблицы, содержащие значения по расчетам передач, валов, шпонок, подшипников и т.п.
Поддерживается возможность настройки обратной связи для этих таблиц, позволяя, таким образом, изменяя значение в таблице, изменять и сам расчет, что намного упрощает и ускоряет работу над проектом. Выводы Cпомощью программ KISSsoft/KISSsys было проведено моделирование и последующий расчёт редуктора при задании выходных параметров. По результатам расчетов была построена 3D-модель редуктора. Чертежи экспортированы в программную систему Pro/ENGINEER и могут быть использованы для дальнейшей работы. Данный проект был выполнен менее, чем за один рабочий день, что свидетельствует о высокой эффективности данного программного продукта в плане экономии времени. Другие публикации в данном разделе:. Посетите наши веб-проекты.